今日kata

原始題目如下:(7kyu)
Given n, take the sum of the digits of n. If that value has more than one digit, continue reducing in this way until a single-digit number is produced. This is only applicable to the natural numbers.

翻譯:
給一自然數n，將每一位數加總(個十百千....)，直到只剩下個位數字

範例:

    16  -->  1 + 6 = 7
   942  -->  9 + 4 + 2 = 15  -->  1 + 5 = 6
132189  -->  1 + 3 + 2 + 1 + 8 + 9 = 24  -->  2 + 4 = 6
493193  -->  4 + 9 + 3 + 1 + 9 + 3 = 29  -->  2 + 9 = 11  -->  1 + 1 = 2

構想&解法

function digital_root(n) {
  while(n>9){
    arr=n.toString().split('')
    n=arr.map(item=>parseInt(item)).reduce((acc,cur)=>acc+cur)
  }
  return n;
}

使用while loop檢查n是否需要做累加。

為了將n的每一位數分開，toString()將數值轉型成字串。(Ex:1234-->'1234')

字串用split()，取得每一位數並存於陣列arr。(Ex:'1234'-->['1','2','3','4'])

陣列用reduce做累加，得到新的n。

再回到while檢查是否符合條件。

其他解法觀摩

function digital_root(n) {
  return (n - 1) % 9 + 1;
}

這個解答獲得Codewars上滿滿的驚呼聲!

• 要知道的是 除以9的特性:
  通常要快速判斷一個數字是不是9的倍數，要將該數字的各個位數相加，如果最後得到的結果為9的倍數，即該數字為9的倍數。EX:57132=5+7+1+3+2=18，1+8=9，9能被9整除，故57132為9的倍數
  由任何一個整數若能被9整除，則該數的各個位數相加也能被9整除
  演化成任何一個整數除以9的餘數一定等於該數的各個位數相加結果除以9的餘數
  忘記這個以前常用的性質也沒關係。

• 推薦另一個影片:說明9的整除The why of the 9 divisibility rule
  其中節錄影片重點:為什麼個位數相加可以拿來判斷是否被9整除

    2934 可以表示成
    = 2 x (1000) + 9 x (100) + 3 x (10) + 4
    = 2 x (1+999) + 9 x (1+99) + 3 x (1+9) + 4
    = 2x999 + 2 + 9x99 +9 + 3x9 + 3 + 4
    =2x999 + 9x99 + 3x9 + 2 + 9 + 3 + 4
    2+9+3+4=18 即為2934除以9的餘數

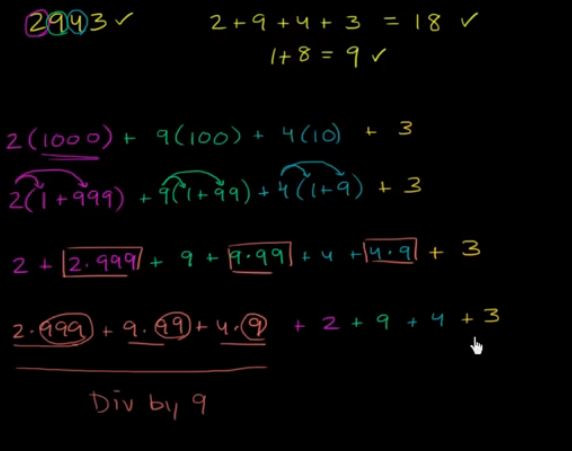
圖摘自The why of the 9 divisibility rule

小結: 任何整數的個位數相加即為除以9的餘數

回到這題要求的將一整數各個位數相加直到結果<10
一樣以2934為例，照題目要求各個位數相加等於2+9+3+4=18，1+8=9，結果回傳9
套用上述提到的9倍數的特性，2934-->18-->9，9%9=0，代表2934能被9整除
但我們要的不是餘數0，而是它相加後的結果
2934-->18-->9
所以先將2934-1，故意讓它除以9的結果產生餘數8，最後再將1加回來
(2934-1)=2933--->17-->8，8%9=8，8+1=9

最後得到有趣的解法

function digital_root(n) {
  return (n - 1) % 9 + 1;
}

以上為今日分享的內容，若有錯誤或是建議，請再隨時和我聯繫